![]()
미술과 수학 교감전
고명근 작 대칭형상의 강렬한 힘
송중덕 작 조형요소
김봉태 작 픽셜이미지 비너스
정광호 작 나무잎속의 프렉탈 기하학
이재호 작 완전함을 상징하는 원
김봉태 작 대칭도형
|
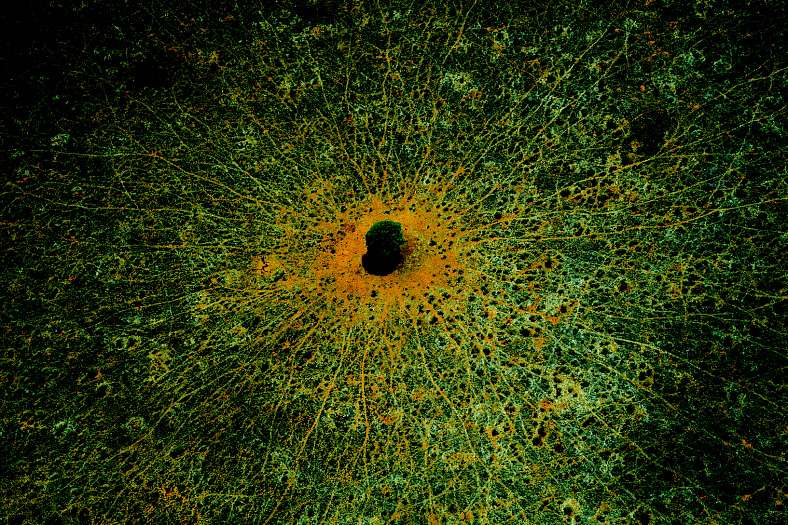
'하늘에서 보이는 땅' 전시회 작품-1
이는 버트란트(Yann Arthus Bertrand)라는 사진작가가 지상 30미터에서 3000미터까지의 고도에서
76개국의 경이로운 자연의 모습들을 3천시간 동안 찍은 작품들. 두 번째 전시회에 선보인 사하라
사막, 히말라야, 몰디브섬, 잉카유적 등 秘境(비경)의 웅대한 아름다움에 입이 벌어집니다. 부분적
으로 이미 보셨을 수도 있지만 아름다운 비경 속에 빠져 그 경이로움을 같이 나누고자 합니다.
일견으로 보기에는 양이 너무 많고 아까워 두 번으로 나눠 띄워 드립니다.^^







































위쪽의 Media Play Button (■) Click Off 후, → 아래의 Media Play Button (▶) Click on!
-플레이 중 창 하단에 뜨는 광고는 우측의 삭제바튼(x)을 클릭하시면 제거됩니다.
-해당 미디어 클립 접속이 많은 시간대에는 화면 끊힘현상이 나타날 수 있습니다.
Interview with God(하나님과의 인터뷰)
The Magician Vs The Golfers (마술과 골프)
The unique talents of the European Tour golfers paired against the skills of magician
Drummond Money-Coutts at Gleneagles Golf Club in Scotland.
|
◈ 늙은 수탉의 흉계 ◈ 100마리의 암탉과 한 마리의 늙은 수탉이 있는 농장에 젊은 수탉은 많은 암탉들을 보면서 이때 터줏대감 늙은 수탉이 "어이~ 신참! 젊은 수탉은 기가 막혔다 엉아!!...그건 너무 하잖아 씨이~ 젊은 수탉은 속으로 (이게 웬 횡재?ㅋㅋ 룰루랄라~) "좋아요! 약속 꼬옥 지켜야 돼요?" 자~ 하나둘셋 하면 뛰는거이야? "허걱! 이런 영감탱이? 이때 "탕! 하는 소리가 나면서..." 그리구... "이상하네? |
배추 아가씨

















사람은 나이 들어 새로운 도전의 꿈을 접는 게 아니라,
새로운 도전에 대한 꿈을 접을 때
시나브로 천천히 그리고 확실히 시들고 늙어 버린다.
-호호야 선문(選文) / 발췌/가필-
 To afford a cup of coffee at ease!
To afford a cup of coffee at ease!Scrapped in places, Edited or Written Partially
by 00000, Sincerely, Private, 1.12, 2013
 선(線 Line)을 분할 하는데, (a+b) : a = a : b 의 비율(比率)이 되도록 분할하는 것을, 기하학에서 황금비율(黃金比率) 또는 황금 분할(黃金分割) 이라고 한다. 선(線 Line)을 분할 하는데, (a+b) : a = a : b 의 비율(比率)이 되도록 분할하는 것을, 기하학에서 황금비율(黃金比率) 또는 황금 분할(黃金分割) 이라고 한다. 이 비율(比率)의 값은 로 계산되어, 1.61803393...:1 (또는 1:0.61803393...) 이 되는데, 바로 이 숫자를 “황금비율 · 황금분할(Golden ratio)” 이라고 한다. 이 황금분할은 기하학적으로 이미 고대 그리스의 유클리드가 정의한 이래 건축, 미술, 예술 분야 등에서 즐겨 응용되어 오고 있다. 어디 그뿐인가? 르네상스 시대의 예술가들은 이 숫자를 “Divine Proportion (신성비율 神性比率)” 이라고 까지 불렀다. 아무튼,이 비율을 이용하여 만들어진 제품은 한없이 많은데... 지금 당장 몸에 지니고 있는 물건 중에서 만년필, 명함, 담배갑 , 신용카드(credit card) 등등도 이에 해당되고... TV 의 Screen(화면)이나 컴퓨터의 모니터(Monitor)에는 16:9 = 1.77778, 15:9 = 1.66667, 5:3 = 1.66667, 16:10 = 1.6 정도의 비율(比率)이 사용되고 있는데, 이것도 결국은 황금비율의 근사치(近似値)이다. 그런데... 이쯤에서 알아두어야 될 것이 있으니... 그것은, 바로,이 숫자가 나오는 또다른 방법이 있다는 사실이다. Fibonacci (Leonardo Fibonacci, c 1170-1240) 라는 사람이 다음과 같은 수열(數列 sequence)를 만들어 놓았다. 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 . . . 별다른 의미가 없어 보이는 이 수열(數列)은 0이라는 숫자에서 부터 시작하여, 바로 앞 자리의 숫자를 합쳐서, 계속 일렬로 나열하여 놓은 것이다. 그런데... 별다른 의미가 있어 보이지 않는 이 수열에서, 두 숫자 간의 비율(比率)을 계산하여 보았더니... 아주 놀란만한 결과가 나오는 것이었다. 즉, 뒤의 숫자를 바로 그 앞의 숫자로 나누어 보면, 어느 경우에나, 그 비율이 거의 일정하게 되어 있었던 것이다. 그런데... 40번 이후의 숫자들 간에는 그 비율이 거의 똑같아서 1.618033988749895 . . . 이었다. 참으로 놀라운 결과였다. 그리하여, 이 숫자 - 1.618033988749895 . . . 를 Fibonacci numbers (휘보나치 숫자) 라고 하는데... Phi (파이) 라고도 부른다. 그런데, 바로, 이 Phi(파이)가 이 글의 앞부분에 나온 황금비율 · 황금분할 (Gold Ratio, Golden Section, or Golden Mean) 의 숫자 - 1.61803393... - 라는 숫자와 거의 같은 것이었다. 그러다 보니, Phi(파이)을 흔히 황금비율 · 황금분할 이라고도 부르게 된 것이다 결론을 내리면 이렇다! “어느 주어진 길이를 가장 이상적으로 둘로 나누는 比率의 근사값이 바로 1.618033 이라는 소리다.” 그리하여... 휘보나치 수열과 Phi(파이) 라는 것이 널리 알려지게 된 것이다. 이것에 대한 것을 좀더 쉽게 설명하여 보면 다음과 같다. 하지만... 이 Phi와 원주율인 Pi와는 서로 다른 것이다. Pi is the ratio of the circumference of a circle to its diameter. 그리고, 원주율을 나타내는 기호 π는 1706년 영국의 수학자 윌리엄 존스에 의해 쓰이기 시작했다. 간단하게 나마... ‘황금비율 · 황금분할’ 과 ‘Phi (파이)에 대한 이야기를 하였는데.... 이에 관한 이야기는 끝없이 계속될 수 있지만, 지면 관계상, 우리가 자연계와 주변에서 흔히 볼수 있는 Phi에 해당되는 현상을 몇가지만 소개하였다. (더 자세한 것은 본인 스스로 알아 보도록 하시라) <출처:閑超 李相奉님 블로그/재편집> |

감사합니다.
*^^*
'호호야' 카테고리의 다른 글
| 부끄러워 말고 가꾸자 (0) | 2013.04.02 |
|---|---|
| 세 가지의 깨달음 (0) | 2013.04.02 |
| 생사관 (0) | 2013.01.25 |
| 행복에 필요한 돈은 얼마? (0) | 2013.01.25 |
| 크리스마스 미니 무대 (0) | 2013.01.25 |





